Pora zabrać się za bardziej złożony przykład, w którym wygenerujemy tablicę zawierającą n elementów. Następnie wylosujemy szukaną wartość, w pętli odszukamy wszystkie elementy tablicy o identycznej wartości, zliczając liczbę wystąpień. Zacznijmy od klasy Random, która umożliwia przeprowadzenie "losowania". W pętli użyjemy metody Next, która oczekuje podania górnego zakresu losowanej wartości. W zmiennej findNumber umieścimy szukaną liczbę. Następnie użyjemy znanej już metody IndexOf, do której oprócz tablicy i szukanej wartości przekażemy indeks pierwszego elementu, od którego mamy zacząć iteracje tablicy. Zmienną findIndex zainicjalizujemy wartością -1 (pierwszy element w tablicy ma indeks 0, a nie chcemy go pominąć). Metoda IndexOf w przypadku nieznalezienia elementu spełniającego warunek zwraca -1. Warunek pętli while jest prawdziwy wyłącznie, gdy metoda zwraca indeks elementu spełniającego warunek większy lub równy 0. W każdym przebiegu rozpoczynamy od ostatnio wyszukanego indeksu + 1. Jeżeli zwrócona zostanie wartość -1 (nie znaleziono elementu spełniającego warunek), pętla kończy działanie. Jeżeli jednak znajdzie się element spełniający warunek, wyświetlimy jego indeks, wykonujemy inkrementację zmiennej countFindNumber zliczającej ilość wystąpień szukanej wartości. Następnie ponownie będziemy iterować tablicę zaczynając od ostatnio wyszukanego indeksu.

using System;

namespace HelloWorld
{
    public static class Program
    {
        public static void Main()
        {
            var r = new Random();

            int countNumber = 1000;
            var numbers = new int[countNumber];

            for (int idx = 0; idx < countNumber; idx++)
                numbers[idx] = r.Next(100);

            int findNumber = r.Next(100);
            int countFindNumber = 0;

            int findIndex = -1;
            while ((findIndex = Array.IndexOf(numbers, findNumber, findIndex + 1)) >= 0)
            {
                Console.WriteLine(findIndex);
                countFindNumber++;
            }

            Console.WriteLine("Number {0} has been found {1} times", findNumber, countFindNumber);
            Console.ReadLine();
        }
    }
}

Poznane metody IndexOf, Find oraz FindAll nie są jedynymi umożliwiającymi wyszukanie indeksu lub elementu. Metody LastIndexOf oraz LastFind umożliwiają wyszukiwanie od tyłu. Inną ciekawą, a zarazem szybką metodą wyszukiwania jest BinarySearch. Jest jeden warunek – tablica musi przechowywać posortowane elementy. Więcej o wyszukiwaniu binarnym możesz przeczytać tutaj.

Kod poniżej to próba zestawienia opisanego już wyszukiwania z wyszukiwaniem binarnym. Do pomiarów wykorzystana zostanie klasa Stopwatch, która udostępnia mechanizm mierzący czas, z dokładnością nazywaną mikropomiarami. Dziwnie wyglądający argument przekazywany do metody ToString to sposób formatowania wartości zwracanej przez mechanizm wykonujący pomiar. O formatowaniu przygotowany zostanie osobny wpis.

using System;
using System.Diagnostics;

namespace HelloWorld
{
    public static class Program
    {
        public static void Main()
        {
            var r = new Random();

            int countNumber = 50000000;
            var numbers = new int[countNumber];
            var sortedNumbers = new int[countNumber];

            var s = new Stopwatch();

            s.Start();
            for (int idx = 0; idx < countNumber; idx++)
                sortedNumbers[idx] = numbers[idx] = r.Next(short.MaxValue);
            s.Stop();

            Console.WriteLine("Time generate tables: {0} with {1} elements", s.Elapsed.ToString(@"ss\.fff"), countNumber);

            //-------------------------------------------------------------------

            s.Restart();
            Array.Sort(sortedNumbers);
            s.Stop();

            Console.WriteLine("Sorted table sortedNumbers: {0}", s.Elapsed.ToString(@"ss\.fff"));
            Console.WriteLine();

            //-------------------------------------------------------------------

            for (int idx = 0; idx < 5; idx++)
            {
                int searchNumber = r.Next(short.MaxValue);

                s.Restart();
                int index = Array.IndexOf(numbers, searchNumber);
                s.Stop();
                var msIndex = s.Elapsed;

                s.Restart();
                Array.BinarySearch(sortedNumbers, searchNumber);
                s.Stop();
                var msBinarySearch = s.Elapsed;

                Console.WriteLine("Search number: " + searchNumber + " (Index: " + index + ")");
                Console.WriteLine("\tIndexOf " + msIndex.ToString("ffffff"));
                Console.WriteLine("\tBinarySearch " + msBinarySearch.ToString("fffffff"));
                Console.WriteLine();
            }

            Console.ReadLine();
        }
    }
}

W uproszczeniu, dla dwóch tablic losujemy identyczny 50-milionowy zbiór elementów. Następnie sortujemy tablicę sortedNumbers. W pętli szukamy 5 losowych liczb. W konsoli wyświetlana jest szukana liczba, jej indeks oraz czasy wyszukania dla każdej z metod. Przyjrzyjmy się zarejestrowanym pomiarom.

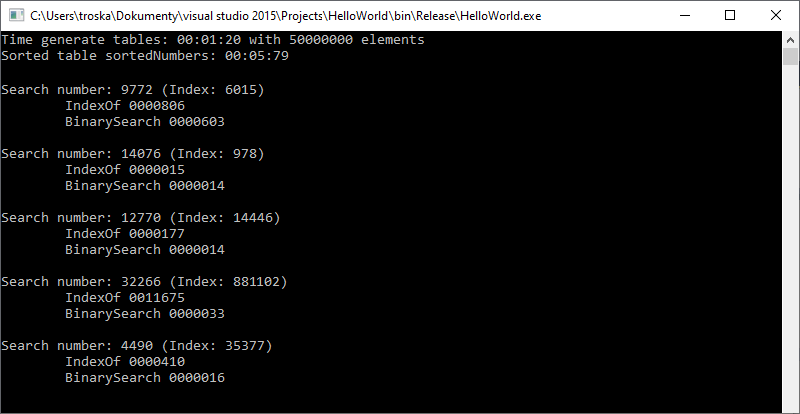
Czas potrzebny na wygenerowanie 50 milionów elementów to około 1,2 sekundy. Metoda IndexOf liniowo przeszukuje elementy tablicy, możemy zauważyć zależność. Im większy indeks elementu w tablicy, tym więcej czasu potrzebujemy na odszukanie elementu. Wartość 14076, która znajduje się na 978 pozycji została wyszukana w czasie 0.0000015 sekundy, w porównaniu do metody BinarySearch jest wolniejsza zaledwie o 0.0000001 sekundy. Jest to przypadek mocno optymistyczny, gdzie szukana wartość znajduje się na początku tablicy. W przypadkach mniej optymistycznych różnica pomiędzy metodami jest "rażąca". Zwróćmy uwagę na wartość 32266, która znajduje się na 881102 pozycji. Wyszukiwanie binarne uporało się w czasie 0.0000033 sekundy, natomiast metoda IndexOf potrzebowała aż 0.0011675 sekundy. W najbardziej pesymistycznym scenariuszu, gdy szukana wartość nie występuje w tablicy metoda IndexOf musi przejść przez wszystkie elementy tablicy, czego nie zrobi metoda BinarySearch.

W przypadku obu metod czas pierwszego użycia jest relatywnie większy, w stosunku do kolejnych prób. Jest to związane z koniecznością przygotowania do działania. Proponuję tak zmodyfikować kod, aby 2 razy dla pierwszego przejścia pętli wyszukać tę samą wartość.

Czy metoda BinarySearch zawsze będzie szybsza? Nie. W sytuacji, gdy tablica będzie zawierała niewiele elementów, złożoność wyszukiwania binarnego może okazać się większa od liniowego przeszukania elementów tablicy. Dodatkowo należy pamiętać o konieczności posortowania tablicy, w tym przypadku czas na sortowanie wyniósł prawie 6 sekund. Wyszukanie 5 elementów z kolekcji 50 milionów, metodą IndexOf, która nie wymaga posortowanych elementów jest szybsze. Podobne rozwiązanie zaimplementowane po stronie serwera np. obsługującego portal www, gdzie w niewielkich odstępach czasu wyszukiwane są kolejne wartości, czas potrzebny na przygotowanie posortowanej tablicy, będzie nieistotny. Metoda BinarySearch jest mniej kosztowna, nie tylko w kontekście czasu. Zwróćmy uwagę na działanie obu algorytmów, a co jest z tym związane na operacje, jakie musi wykonać procesor podczas przeszukiwania.

Troska Robert